How Batch Normalization Works and What It Is

The central problem that Batch Normalization (BN) aims to solve in the field of deep learning is known as “internal covariate shift”. To fully understand the significance of this solution, it’s crucial to analyze the nature of the problem and the way BN acts effectively to mitigate it.

What Is Internal Covariate Shift?

Internal covariate shift refers to the changes in the distribution of inputs to the various layers of a neural network during the training process. As the network adjusts and learns from the data, the weights and biases of the layers are updated, causing a continuous shift in the distributions of inputs received by subsequent layers. This phenomenon forces each layer of the network to constantly adjust to new distributions, slowing down the model’s convergence and making the training process more difficult.

Why Is Internal Covariate Shift a Problem?

The continuous change in input distributions makes it difficult for the network to stabilize learning, as the layers must constantly adapt to new conditions. This not only slows down training but also complicates the tuning of network parameters, such as the learning rate and weight initialization. Moreover, it can lead to saturation issues in activation functions (e.g., sigmoid and tanh functions), where too high or too low input values reduce the network’s sensitivity to variations in input data.

How Does Batch Normalization Work?

Batch Normalization addresses the problem of internal covariate shift by normalizing the inputs to each layer for every batch of data. In practice, this means adjusting the inputs of layers so that they have a mean close to zero and a unit variance. This process stabilizes the distributions of inputs for subsequent layers, allowing the network to learn more efficiently.

The BN process follows these steps:

1. Calculation of Mean and Variance: For each batch of data, BN calculates the mean and variance of the inputs to a layer.

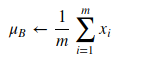
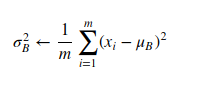
2. Normalization: The inputs are then normalized by subtracting the mean and dividing by the square root of the variance plus a small epsilon term, to avoid division by zero.

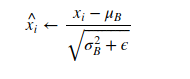
3. Scaling and Translation: Finally, the normalized inputs are scaled and shifted through learned parameters.

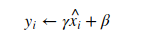
where y is the normalized value produced by each sub-layer of the network that will pass through the activation function, such as Sigmoid, Relu, Tanh, etc.

These steps allow BN to maintain the network’s ability to represent nonlinear functions.

Advantages of Batch Normalization

Stabilizing input distributions through BN leads to numerous advantages:

• Acceleration of Training: By reducing internal covariate shift, BN allows for the use of higher learning rates without the risk of divergence, significantly speeding up training.
• Improved Initialization: With BN, the network becomes less sensitive to weight initialization.
• Efficient Use of Nonlinear Activation Functions: BN reduces the risk of saturation for activation functions like sigmoid, enabling the construction of deeper neural networks.
• Regularization Effect: BN introduces a slight regularization effect, potentially reducing the need for other techniques such as dropout.