
In questo articolo continueremo ad approfondire l’algebra lineare ed in particolare, inizieremo a vedere alcune operazioni che possono essere fatte sui tensori. Per semplicità, utilizzeremo per gli esempi successivi solo tensori 2D (bidimensionali) ovvero matrici. In questo articolo, tratteremo, in particolare l’operazione di moltiplicazione tra tensori. Il prodotto tra matrici, detto anche prodotto riga per colonna, è una delle operazioni tra matrici più delicate. A differenza della moltiplicazione tra scalari il prodotto tra matrici non è commutativo e si può eseguire solo in certe condizioni. Quando si può svolgere, esso restituisce una matrice avente tante righe quante sono quelle della prima matrice e tante colonne quante sono quelle della seconda. Quindi nell’esempio seguente:
il risultato della moltiplicazione sarà una matrice 2X3. Per moltiplicare due matrici, esse devono essere dimensionalmente compatibili, cioè la prima matrice dovrà avere lo stesso numero di colonne delle righe della seconda matrice.Nel nostro esempio la prima matrice, infatti, ha shape 2X3 mentre la seconda matrice ha shape 3×3. Per capire se le due matrici sono compatibili per la moltiplicazione, possiamo usare un metodo molto semplice, basterà scrivere lo shape delle matrici e verificare se i termini intermedi sono uguali. Nel nostro caso avremo : 2X3 3X3 e quindi le matrici sono compatibili per la moltiplicazione. Ma quale sarà il risultato?
Bene il risultato sarà una matrice 2X3 del tipo:
dove :
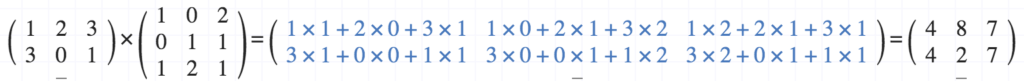

Sono amante della tecnologia e delle tante sfumature del mondo IT, ho partecipato, sin dai primi anni di università ad importanti progetti in ambito Internet proseguendo, negli anni, allo startup, sviluppo e direzione di diverse aziende; Nei primi anni di carriera ho lavorato come consulente nel mondo dell’IT italiano, partecipando attivamente a progetti nazionali ed internazionali per realtà quali Ericsson, Telecom, Tin.it, Accenture, Tiscali, CNR. Dal 2010 mi occupo di startup mediante una delle mie società techintouch S.r.l che grazie alla collaborazione con la Digital Magics SpA, di cui sono Partner la Campania, mi occupo di supportare ed accelerare aziende del territorio .
Attualmente ricopro le cariche di :
– CTO MareGroup
– CTO Innoida
– Co-CEO in Techintouch s.r.l.
– Board member in StepFund GP SA
Manager ed imprenditore dal 2000 sono stato,
CEO e founder di Eclettica S.r.l. , Società specializzata in sviluppo software e System Integration
Partner per la Campania di Digital Magics S.p.A.
CTO e co-founder di Nexsoft S.p.A, società specializzata nella Consulenza di Servizi in ambito Informatico e sviluppo di soluzioni di System Integration, CTO della ITsys S.r.l. Società specializzata nella gestione di sistemi IT per la quale ho partecipato attivamente alla fase di startup.
Sognatore da sempre, curioso di novità ed alla ricerca di “nuovi mondi da esplorare“.

